Blog:20250925-Hexagons

The Beauty of Hexagons

Posted on 24 September 2025

For me, hexagons are beautiful - simple geometric shapes that feel magical. They can look organic or artificial, venerable or futuristic, stable or flexible, but they are always elegant and efficient.

Maybe I'm a bit biased. I've always associated hexagons with games, which is why they are part of some of my favorite memories. Losing my first strategy games to my big brother (but at least I got to play!), and the many rounds of Settlers of Catan with good friends. Some of the best games ever made use hexagonal boards. But why are hexagons so popular in game design? There's a good reason.

Hexagonal Grids

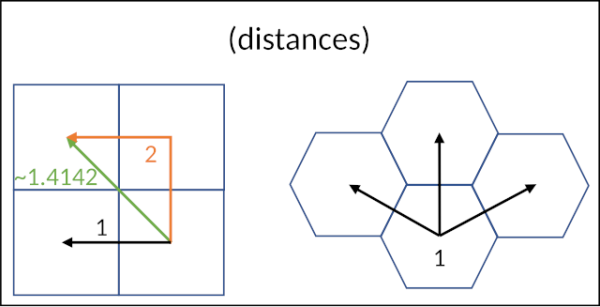
Imagine a game board made of hexagons instead of squares. In a hexagonal grid, every hexagon has six neighbors, and the distance to each is exactly the same.

Now, think about a classic square grid. A square has eight neighbors: four on the sides and four on the corners. If you only move to the sides, each step is the same length. But if you move diagonally to a corner, the distance is about 1.4 (√2) times longer.

Is this a problem? Not always. In games like chess, it’s a feature. The different movement rules for each piece work perfectly with this type of grid. However, if you need pieces to move freely over a fixed distance, a square grid has its limits. If you only allow side-to-side moves, you can't get to certain squares as easily. If you allow diagonal moves, your steps are no longer the same length.

Hexagonal grids solve this problem. While a perfectly straight path isn't always possible, the six directions available in a hex grid allow for a much better approximation of a straight line. The difference between a true straight line and a path on a hex grid is at most 15.5%, compared to up to 41.4% on a square grid that allows diagonal movement. And every step is always the same distance.

Hex grids aren't perfect, of course. It's harder to make rectangular shapes like buildings and corridors with hexagons, which can complicate movement rules. They also have more complex coordinate systems. Luckily, there are practical solutions for this.

Coordinate Systems for Hexagons

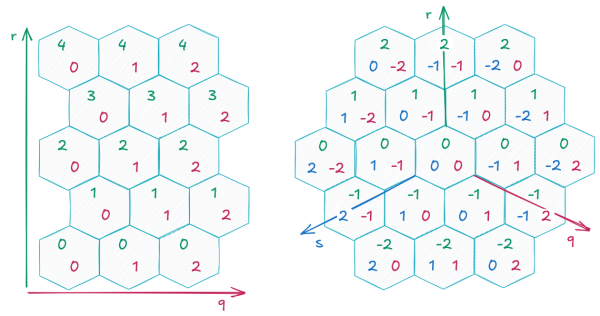
It's easy to plot points on a square grid. You use a simple x and y axis, with the x value for the column and the y value for the row. You learn this basic math in school.

But how does this work with hexagons? You still have columns (q) and rows (r). However, because of the hex shape, some neighbors are offset. If you arrange the hexagons with a point at the top, every other row is shifted to the right. This is called an offset coordinate system. While it works, it doesn't allow for the same kind of easy calculations as a square grid.

An elegant solution is to use a 3D coordinate system. You can project a 3D grid onto your 2D hex grid. Each coordinate then lines up with a row of hex fields. This is called cube coordinates. This system allows you to use standard calculations like addition and multiplication, making it much easier to figure out distances and plot paths.

Overlapping Hex Grids

Sometimes in game design, you want to use different grid sizes on the same map. For example, you might want a larger grid to represent major areas like biomes or islands, and a smaller grid to show the individual fields within those areas. With square grids, this is simple: you can just divide a larger square into four, nine, or any squared number of smaller squares that align perfectly.

However, this doesn't work with hexagons. You can't perfectly slice one hexagon into smaller ones without having leftover areas.

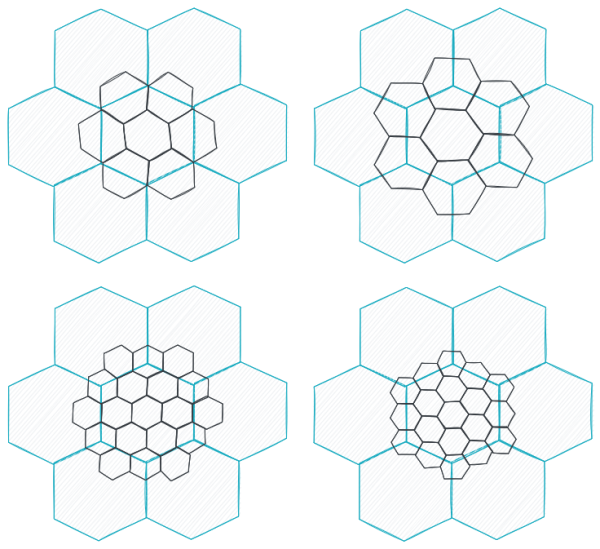
To solve this, you can allow the smaller fields to overlap multiple larger hexagons. This creates a few different types of sub-fields. You get "inner" hexagons that are fully enclosed by a single larger parent hexagon, and "outer" or "fringe" hexagons that sit on the borders between two or three larger parents. The way these overlap depends on whether the hexagons are oriented with a pointy-top or a flat-top.

In Exsol, I use a pointy-top grid for the larger station sectors and a smaller flat-top grid for the subsectors within. This setup gives me three types of subsectors:

• Inner subsectors: The seven fields completely enclosed within a single sector.
• Outer subsectors: The six fields that mark the border between two neighboring sectors.
• Corner subsectors: The six fields that lie between three neighboring sectors.

Conclusion

This blog post provides a brief introduction to hexagonal grids and how they can be used in game design. Going forward, this will help you understand some of the design choices I’ve made while building Exsol. If you’re interested in learning more about hexagonal grids and cube coordinates, I highly recommend this great guide by Amit Patel. And if you're still not convinced of the beauty of hexagons, please take a look at this excellent piece of art.