Blog:20250716-Hexagons: Difference between revisions
No edit summary |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 19: | Line 19: | ||
== Coordinate systems for hexagons == | == Coordinate systems for hexagons == | ||
[[File:Hexagons-cube-coordinates. | [[File:Hexagons-cube-coordinates.png|right|700px]] | ||
The gridding of square-based game boards is trivial. Here we have two axes, usually x and y, which are at right angles to each other. The x value describes the column number and the y value describes the row number of a square. The basic calculations within this Cartesian coordinate system are taught early on in school. So far, so good. | The gridding of square-based game boards is trivial. Here we have two axes, usually x and y, which are at right angles to each other. The x value describes the column number and the y value describes the row number of a square. The basic calculations within this Cartesian coordinate system are taught early on in school. So far, so good. | ||
| Line 25: | Line 25: | ||
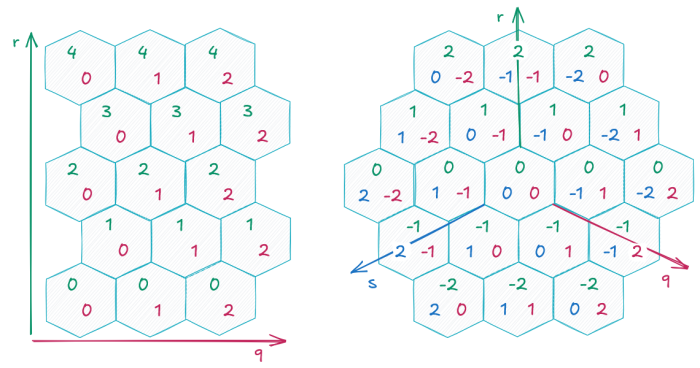
But how does this translate to a hexagon-based grid? Well, here too we have columns (q) and rows (r). However, due to the shape of a hexagon, some neighbors are offset, meaning they are not directly below or next to each other. If you arrange the hexagons with the tip pointing upwards, every second row is offset to the right by half the width. If you point the tip to the right, every second column is offset. This arrangement is called offset coordinates. In principle, we can work with this type of coordinates. However, they do not support the use of vector operations as in a 2D Cartesian coordinate system. | But how does this translate to a hexagon-based grid? Well, here too we have columns (q) and rows (r). However, due to the shape of a hexagon, some neighbors are offset, meaning they are not directly below or next to each other. If you arrange the hexagons with the tip pointing upwards, every second row is offset to the right by half the width. If you point the tip to the right, every second column is offset. This arrangement is called offset coordinates. In principle, we can work with this type of coordinates. However, they do not support the use of vector operations as in a 2D Cartesian coordinate system. | ||
There is an elegant solution to this problem. We can project a three-dimensional coordinate system onto our hex grid. Each coordinate correlates with a line of hex fields on the grid. When we increase a coordinate by 1, we move from one line to the next one that runs parallel to it. The beauty of this system is that it allows us to adapt vector operations as in a 3D Cartesian coordinate system. | There is an elegant solution to this problem. We can project a three-dimensional coordinate system onto our hex grid. Each coordinate correlates with a line of hex fields on the grid. When we increase a coordinate by 1, we move from one line to the next one that runs parallel to it. The beauty of this system is that it allows us to adapt vector operations as in a 3D Cartesian coordinate system such as addition and multiplication. It is also very easy to apply algorithms for calculating distances and pathfinding. If you are interested in hexagonal grids and cube coordinates, have a look at this great [https://www.redblobgames.com/grids/hexagons/ introduction] by Amit Patel. | ||
Latest revision as of 15:58, 25 August 2025
The beauty of hexagons

Hexagons are beautiful! For me, they are little masterpieces. A simple geometric shape that somehow conveys something magical. Depending on the context, they are organic or artificial, historical or futuristic, stable or flexible, but always elegant and efficient.
Maybe my view is a bit biased. I've always associated hexagons with games of all kinds and that's why they are part of some of my fondest memories. The first strategy games I had to lose to my big brother. But hey, at least I got to play with him. And the many rounds of Settlers of Catan at the table with good friends. That's where friendships were put to the test. Some of the best games of all time rely on hexagonal boards. But why are hexagons so popular in game design? Well, there's a good reason.
Hexagonal grids
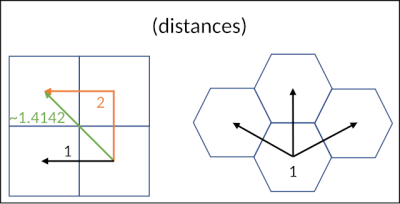
If you arrange squares on a game board as equilateral hexagons, then all neighboring squares are equidistant from each other. This means that each hexagon has six neighbors and the path to each of them is the same. Compare this to a classic game board consisting of squares. Here, each square has eight neighbors, four on each side and four diagonally. So the first question is how a piece can be moved here. If you only move across the sides, each step covers the same distance. However, if you want to move diagonally, the distance is √2 times (about 1.42 times) that of the other neighbors.
Is that a bad thing? In many cases it is not. In games like chess, it's even a feature. The different movements of the pieces are designed for exactly this kind of grid and harmonize wonderfully with it. Real distances don't play a role here. However, if game pieces need to be able to move as freely as possible over a fixed distance, then a grid of squares quickly reaches its limits. If you only allow movement across the horizontal and vertical neighbors, the distance to squares in between increases enormously. If you also allow movement across the diagonal, you can no longer divide movements into equally sized steps.
Hexagonal grids reduce the first problem and eliminate the second. Even with hexagonal grids, there is not always a linear path from one hex to another. However, the six possible basic directions allow a much better approximation. The largest possible deviation here is 15.5 % compared to a maximum of 41.4 % for squares that allow diagonal movement. And the individual steps are always the same distance. Of course, hexagonal grids are not perfect either. An obvious disadvantage is that the hexagonal shape of the fields makes it more difficult to depict rectangular structures such as buildings and corridors. Here you often have to work with split fields, which complicates the movement rules in a game. Another disadvantage is that the coordinate systems for hexagons are somewhat more complex. Fortunately, there are practicable solutions for this.
Coordinate systems for hexagons
The gridding of square-based game boards is trivial. Here we have two axes, usually x and y, which are at right angles to each other. The x value describes the column number and the y value describes the row number of a square. The basic calculations within this Cartesian coordinate system are taught early on in school. So far, so good.
But how does this translate to a hexagon-based grid? Well, here too we have columns (q) and rows (r). However, due to the shape of a hexagon, some neighbors are offset, meaning they are not directly below or next to each other. If you arrange the hexagons with the tip pointing upwards, every second row is offset to the right by half the width. If you point the tip to the right, every second column is offset. This arrangement is called offset coordinates. In principle, we can work with this type of coordinates. However, they do not support the use of vector operations as in a 2D Cartesian coordinate system.
There is an elegant solution to this problem. We can project a three-dimensional coordinate system onto our hex grid. Each coordinate correlates with a line of hex fields on the grid. When we increase a coordinate by 1, we move from one line to the next one that runs parallel to it. The beauty of this system is that it allows us to adapt vector operations as in a 3D Cartesian coordinate system such as addition and multiplication. It is also very easy to apply algorithms for calculating distances and pathfinding. If you are interested in hexagonal grids and cube coordinates, have a look at this great introduction by Amit Patel.
